**正则化 L1 与 L2 的区别:详细说明**
正则化是机器学习中的重要技术,用于防止过拟合和提高模型的泛化能力。其中,L1 和 L2 正则化是两种常用的方法,它们具有不同的特性和应用场景。
一、L1 正则化(Lasso 回归)
L1 正则化,也称为 Lasso 回归,通过在损失函数中添加权重系数之和惩罚项来限制模型中权重的大小。L1 正则化的目标函数如下:
```
Loss(w) = Original Loss Function + λ * Σ|w|
```
其中:
* Loss(w) 为损失函数
* w 为模型权重
* λ 为正则化参数,用于控制正则化强度
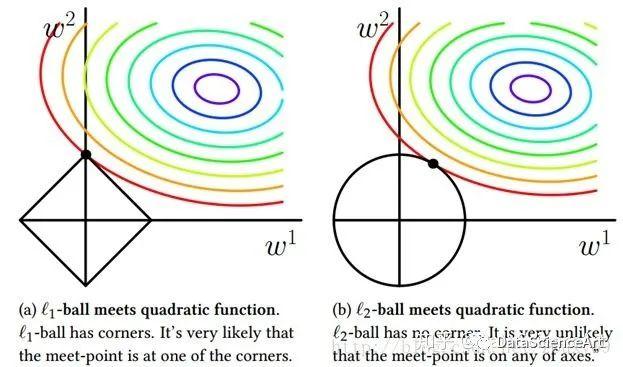
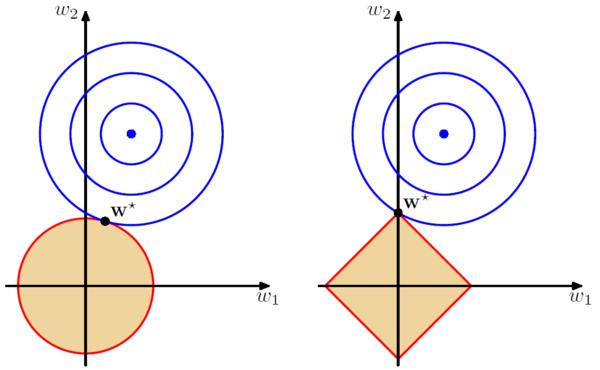
L1 正则化的特点是,它倾向于将模型中一些权重完全归零。这样可以实现特征选择,即识别出对模型预测贡献较大的相关特征。
二、L2 正则化(Ridge 回归)
L2 正则化,也称为 Ridge 回归,通过在损失函数中添加权重系数平方和惩罚项来限制模型中权重的大小。L2 正则化的目标函数如下:
```
Loss(w) = Original Loss Function + λ * Σw^2
```
其中:
* Loss(w) 为损失函数
* w 为模型权重
* λ 为正则化参数,用于控制正则化强度
与 L1 正则化不同,L2 正则化不会将权重归零。相反,它倾向于缩小所有权重的值,从而使模型更加稳定。
三、L1 与 L2 正则化的选择
L1 和 L2 正则化在选择上主要取决于问题的具体情况:
* **L1 正则化**适用于特征数量较多、特征相关性较强的问题。它可以实现特征选择,提高模型的解释性。
* **L2 正则化**适用于特征数量较少、特征相关性较弱的问题。它可以提高模型的稳定性,减少过拟合的风险。
L1 正则化计算成本较高,而 L2 正则化计算成本较低。因此,在特征数量较多时,L2 正则化通常是更合适的选择。
**结论**
L1 和 L2 正则化是机器学习中两种重要的正则化方法,具有不同的特性和应用场景。L1 正则化倾向于进行特征选择,而 L2 正则化则更关注模型的稳定性。通过理解它们的差异,我们可以根据具体问题选择最合适的正则化方法,提高模型的泛化能力和预测准确性。